
Heron’s Formula Definition, Proof, Examples, Application
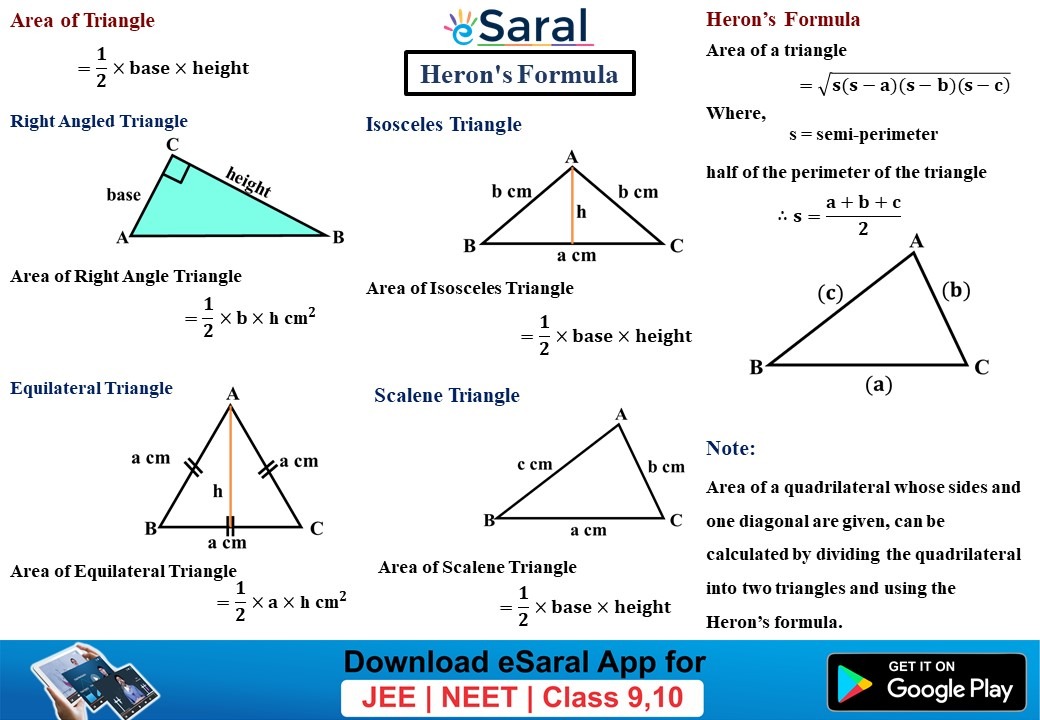
The steps to determine the area using Heron's formula are: Step 1: Find the perimeter of the given triangle. Step 2: Find the semi-perimeter by halving the perimeter. Step 3: Find the area of the triangle using Heron's formula √(s(s - a)(s - b)(s - c)). Step 4: Once the value is determined, write the unit at the end (For example, m 2, cm 2, or in 2). Heron's Formula for Equilateral Triangle
Heron’s Formula Practice Problems With Answers ChiliMath
The perimeter of a triangle is its three sides added together. The area of a triangle is quite interesting. It will usually be expressed as area = (1/2) x base x height, A = (1/2)b*h, where height is measured as a vertical line from the base to the opposite vertex.This formula makes calculating the area of a triangle relatively easy, but it is quite difficult to naturally find a triangle that.

Heron's Formula Explanation and Example YouTube
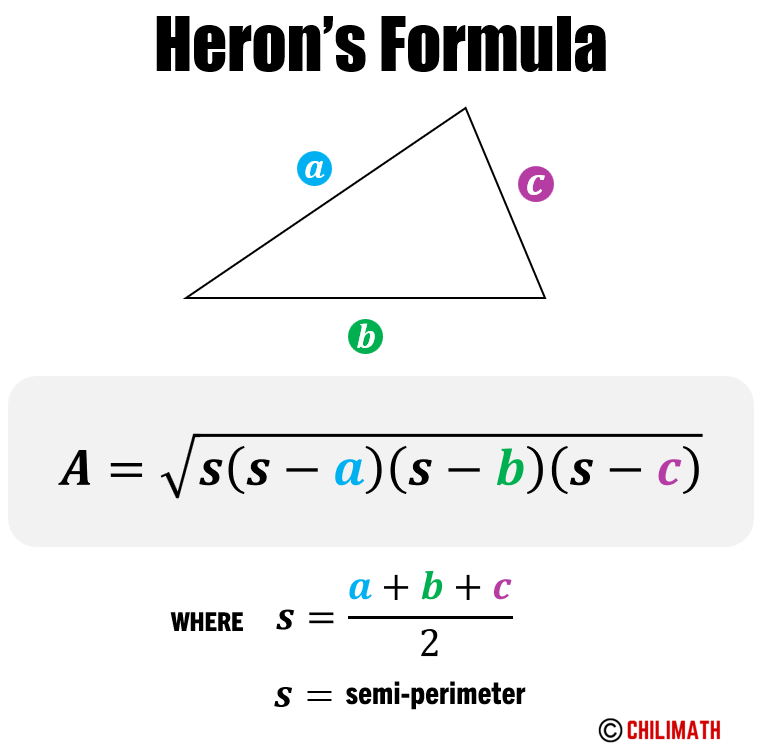
Heron's Formula to Calculate Area of Triangle. Heron's Formula is a clever method for calculating the area of a triangle. It does not require the triangle's height to compute the area; instead, it requires the lengths of the three sides which are easier to find. In the formula, the sides of the triangle are labeled as [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
FormulasHeron's Formula Media4Math
I will assume the Pythagorean theorem and the area formula for a triangle. is the length of a base and is the height to that base. so, for future reference, 2s = a + b + c 2 (s - a) = - a + b + c 2 (s - b) = a - b + c 2 (s - c) = a + b - c. There is at least one side of our triangle for which the altitude lies "inside" the triangle.

Heron's Formula YouTube
Heron's Formula for the area of a triangle. (Hero's Formula) A method for calculating the area of a triangle when you know the lengths of all three sides. Let a,b,c be the lengths of the sides of a triangle. The area is given by: Try this Drag the orange dots to reshape the triangle. The formula shown will re-calculate the triangle's area using.

heron's formula calculator
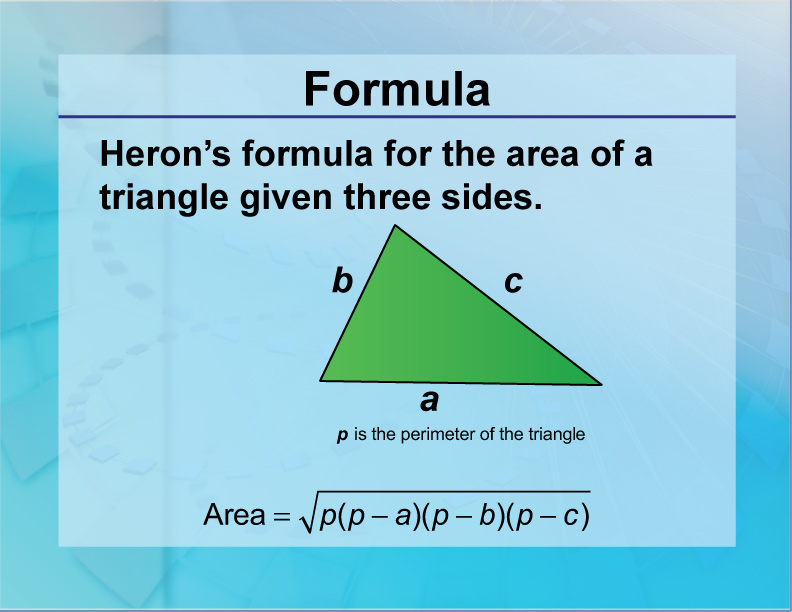
Heron's formula is a formula to calculate the area of triangles, given the three sides of the triangle. This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal. If a, b and c are the three sides of a triangle, respectively, then Heron's formula is given by:

Heron’s Formula Area of a Triangle Knowing Lengths of 3 Sides Algebraic Proof — Steemit
You can calculate the area of a triangle if you know the lengths of all three sides, using a formula that has been known for nearly 2000 years. It is called "Heron's Formula" after Hero of Alexandria (see below) Just use this two step process: Step 1: Calculate "s" (half of the triangles perimeter): s = a+b+c 2. Step 2: Then calculate the Area:
Heron’s Formula Class 9 Maths Chapter 10 Short Notes (Mind Maps)
Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

Herons formula Class 9 Maths CBSE ICSE FREE Tutorial YouTube
8 Heron's Proof… Heron's Proof n The proof for this theorem is broken into three parts. n Part A inscribes a circle within a triangle to get a relationship between the triangle's area and semiperimeter. n Part B uses the same circle inscribed within a triangle in Part A to find the terms s-a, s-b, and s-c in the diagram. n Part C uses the same diagram with a quadrilateral
PPT Heron’s formula PowerPoint Presentation, free download ID1033929
HERON'S FORMULA 135 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 10.6). The advertisements yield an

Heron's Formula Khan academy, Heron, Geometry
Octopus K-12 SD card solution provides educational help to the students of class 1 to 12. The device-specific application for Android provides high-quality a.

Heron’s Formula — Find Area of a Triangle Using Lengths of Its Sides (Example, Formula
The steps to find the area of a triangle using Heron's formula are as follows: Step 1: Find the perimeter of the given triangle. Step 2: Calculate the semi-perimeter (s) of the triangle by adding the three side lengths and dividing by 2. s = a + b + c 2. Step 3: Use Heron's formula to find the area (A) of the triangle.

Heron’s Formula Definition, Proof, Examples, Application
CBSE Class 9 Maths Notes Chapter 7 Heron's Formula. 1. Triangle: A plane figure bounded by three line segments is called a triangle. In ΔABC has. (i) three vertices, namely A, B and C. (ii) three sides, namely AB, BC and CA. (iii) three angles, namely ∠A, ∠B and ∠C.

Heron's Formula Proof (finding the area of ANY triangle) YouTube
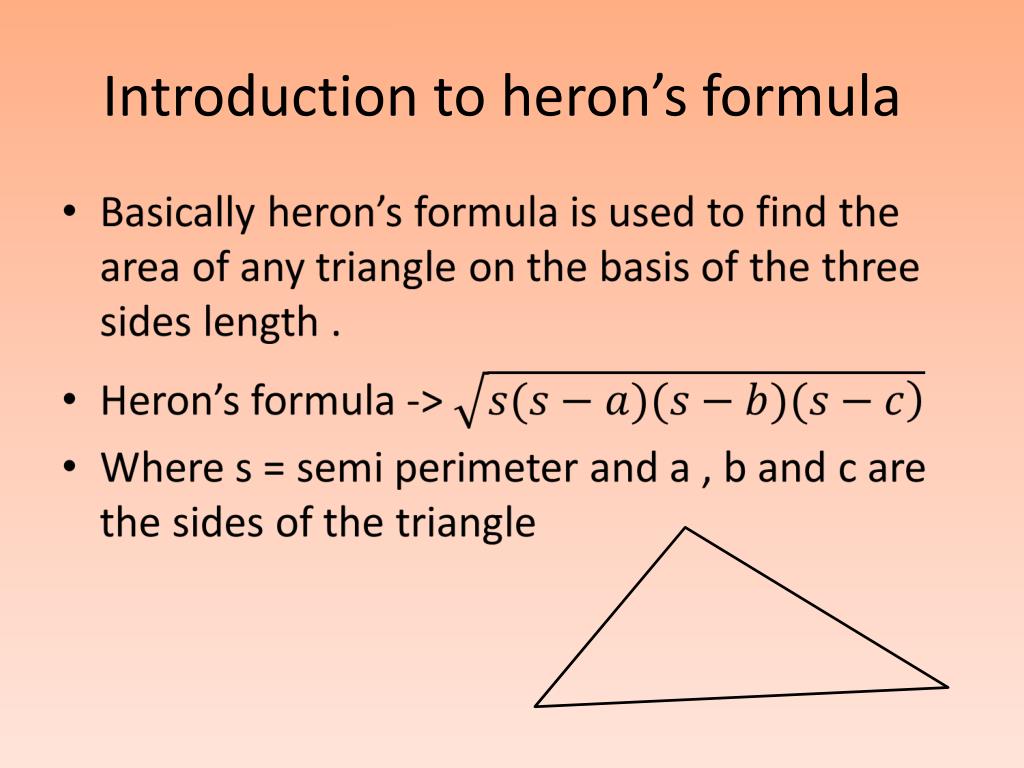
Heron's Formula: Heron of Alexandria was a Greek mathematician.Heron has derived the formula for the area of a triangle when the measure of three sides is given. Unlike the other formula for triangles, we need not calculate angles or other parameters of the triangle while using Heron's formula.

Proof of Heron's Formula YouTube
NCERT Solutions Class 9 Maths Chapter 12 - Download Free PDF *According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10. NCERT Solutions for Class 9 Maths Chapter 12 - Heron's Formula is provided here. Heron's formula is a fundamental concept that finds significance in countless areas and is included in the CBSE Syllabus of Class 9 Maths.

Heron's formula basic to advanced explanation YouTube
Heron's formula is named after Hero of Alexendria, a Greek Engineer and Mathematician in 10 - 70 AD. You can use this formula to find the area of a triangle using the 3 side lengths.. Therefore, you do not have to rely on the formula for area that uses base and height.Diagram 1 below illustrates the general formula where S represents the semi-perimeter of the triangle.